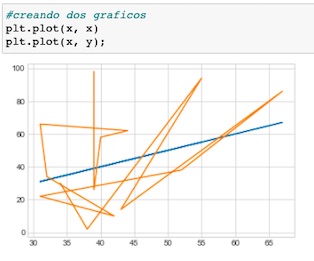
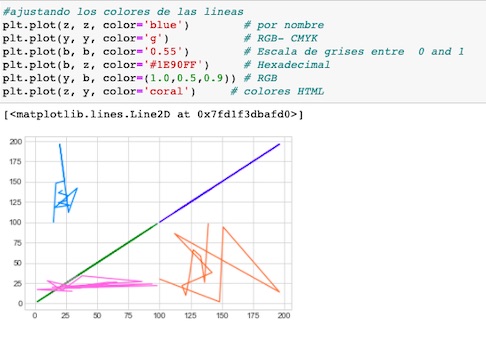
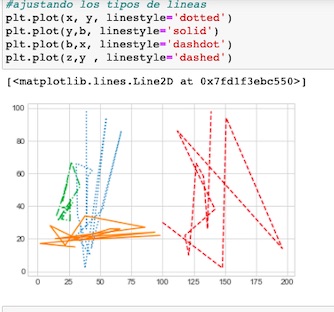
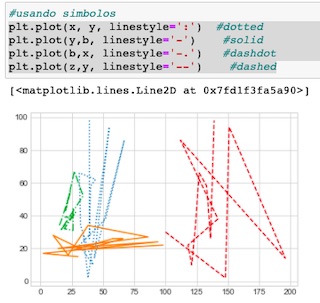
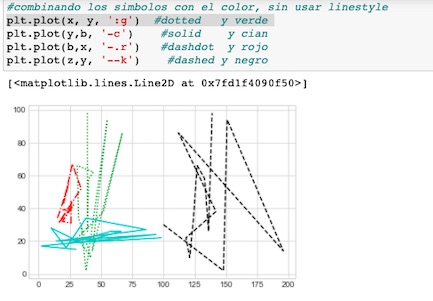
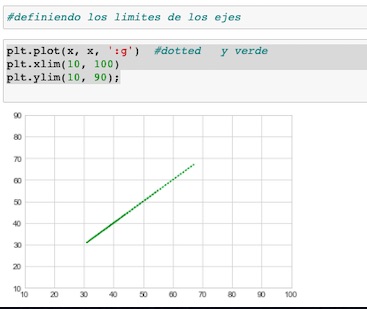
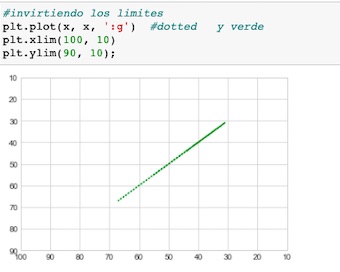
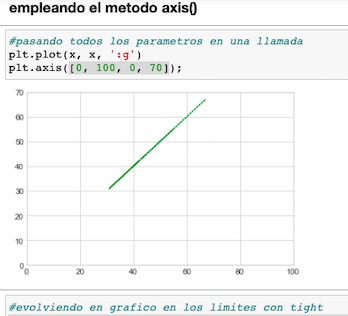
En este post realizaré un análisis de regresión, en el que tomaremos una set de datos preparado previamente.
El problema real al que nos enfrentamos, es determinar la relación que pueda existir entre la cantidad de ventas de la empresa “El Dorado”, y el numero de vendedores que la han integrado durante el periodo que se estudia, que son 36 meses o sea los últimos 3 años.
El departamento ha cambiado de responsable en varias ocasiones, y cada uno ha aplicado políticas diferentes de ventas, algunas intensivas, buscando mayor productividad en las ventas, a bases de estímulos como bonos, primas, ascensos, etc; y en otras ocasiones, en cambio, se han aplicado medidas extensivas incrementando el numero de vendedores, en una afán por ampliar la cobertura de ventas.
Lo que vamos a hacer es implementar un análisis de regresión lineal.
La regresion lineal es una técnica estadística, que el machine learning adoptó y que incluye como uno de los algoritmos supervisados.
He escrito hace unos meses algún articulo sobre regresion lineal y resumiendo lo que hara este análisis es obtener una recta que se acerque lo mas posible a todos los puntos de datos representados en un plano.
En nuestro caso es una regresion simple (participan dos variables ) y la recta que buscamos obtener es, la mejor posible.
Esto quiere decir que de todas las rectas esta sea la que mejor se adapte al conjunto de puntos, lo que le permitirá tendencialmente estimar o predecir valores, dentro del contexto de datos estudiados.
La recta tiene forma esta forma Y = mX + b; donde Y es el resultado obtenido, X es la variable, m la pendiente (o coeficiente) de la recta y b el valor constante, que gráficamente expresa el “punto donde cuando X tiene valor cero, se produce la intercepción o corte con el eje Y.
Su optimización o ajuste se logra aplicándole una función llamada de mínimos cuadráticos, o también conocida de error cuadrático.
Su nombre obedece a que esa funcion intenta minimizar el error existente entre los puntos o dados y los obtenidos, elevendo al cuadrado sus valores para evitar que se anulen.
De este modo el algoritmo, se centra en minimizar el coste de dicha función
Recordemos que los algoritmos de Machine Learning Supervisados, aprenden por sí mismos.
Utilizaremos un archivo de datos que ya tenemos, y que muestra el número de ventas y vendedores por meses; o sea tendremos dos columnas: vendedores y ventas.
Y nuestro en nuestro análisis de regresión, lo que vamos a intentar es determinar a partir de los vendedores que tenemos, que valor podemos esperar en la ventas de acuerdo, a la relación dada entre ambas variables.
Trabajaremos con Jupiter Notebook,utilizaremos las librerías Pandas, SkLearn, Seaborn, Numpy, de modo que comenzaremos por ahí.
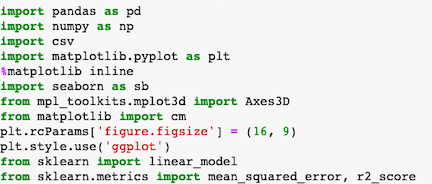
Importamos las librerías
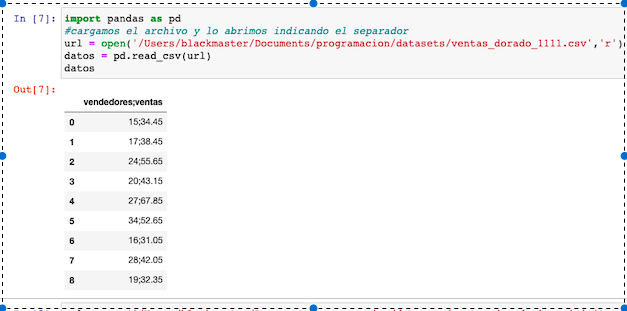
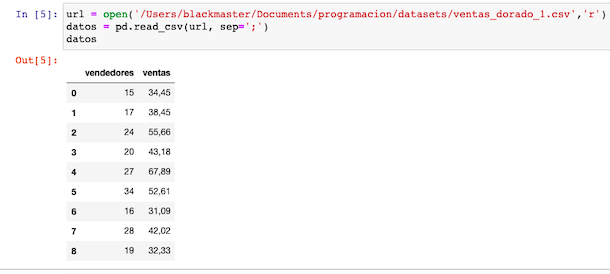
Cargamos nuestro archivo en un dataset de pandas después de leerlo, definiendo el separador de columnas.

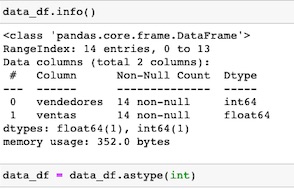
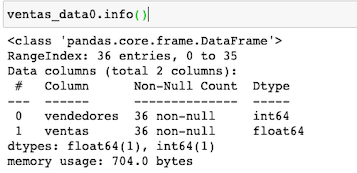
Adquirimos la información de nuestro dataset, con el método info(). Observamos que tenemos dos tipos de datos : enteros en columna vendedores y decimales en la columna ventas.
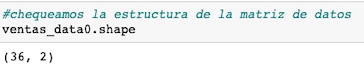
Comprobamos la estructura del dataset, con el método shape, que nos dice que tenemos efectivamente dos columnas y 36 registros en cada una.
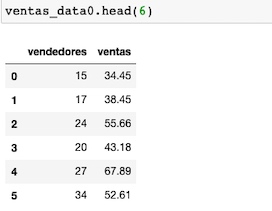
Con head(), visualizamos las 6 primeras filas de nuestro dataset
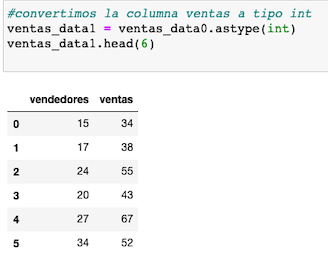
Convertimos por comodidad la columna venta a tipo entero, empleando el método astype() y guardamos esa transformación en un nuevo dataset, que es con el que continuaremos trabajando.
Definimos con columns(), los encabezados de las columnas

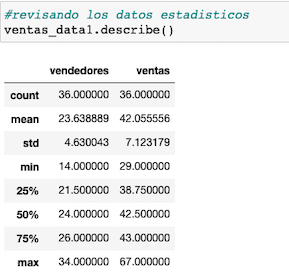
Obtenemos los valores estadísticos de nuestro dataset con el método describe()
Observamos entre otros valores, que la media de vendedores es 23, con una desviación de 4,63; mientras que la de ventas es 42 millones y su desviación es de 7.12.
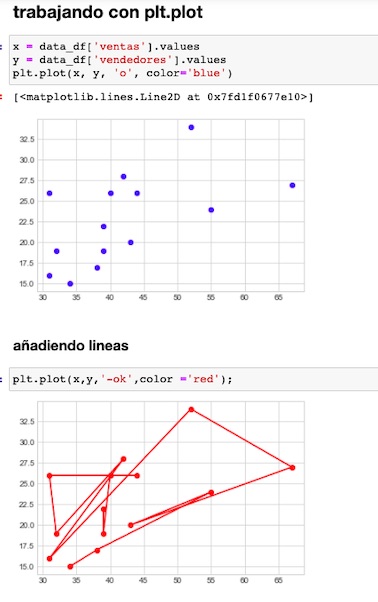
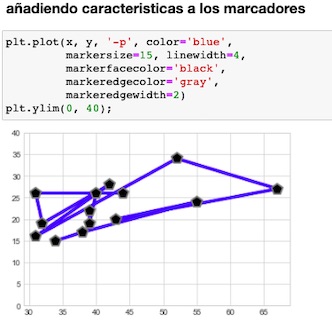
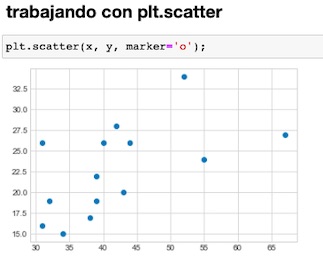
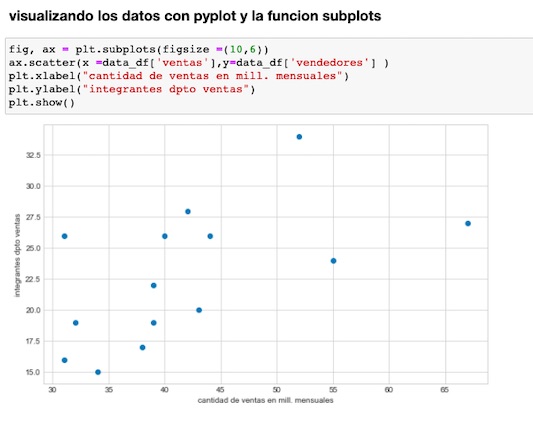
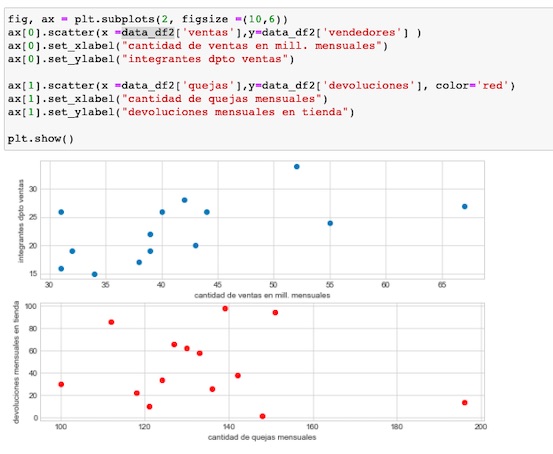
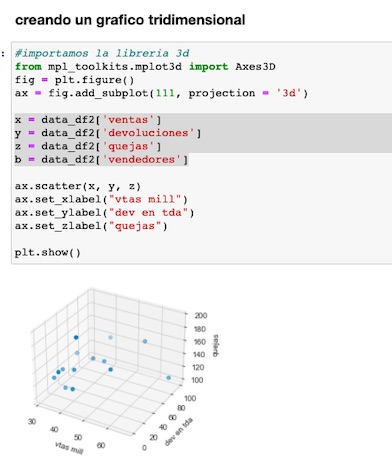
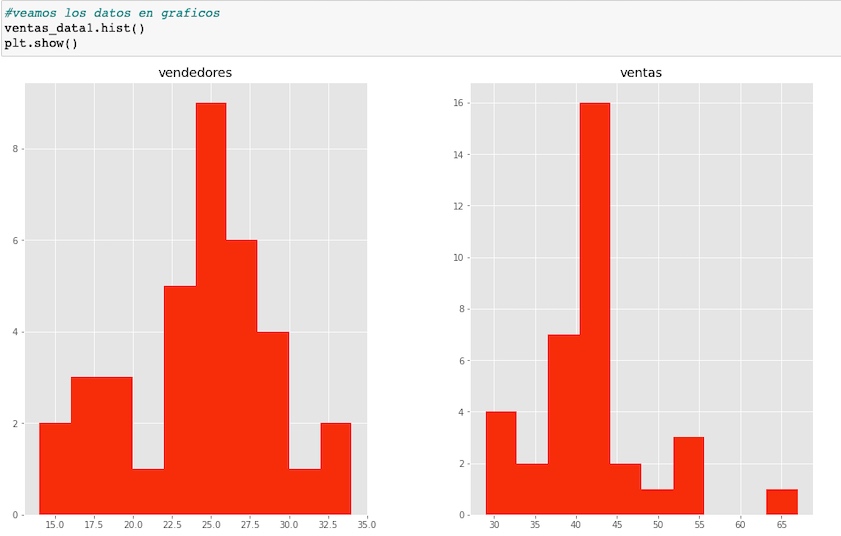
Visualizamos los datos, en gráficos, mostrando las columnas por separados
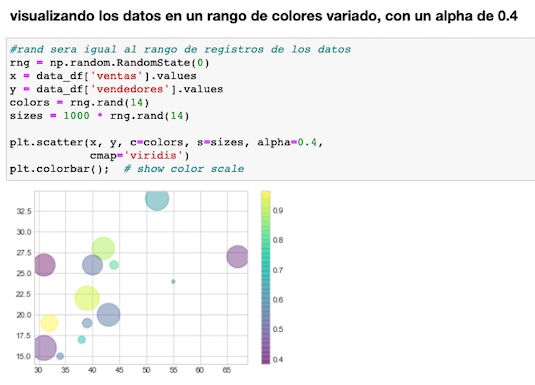
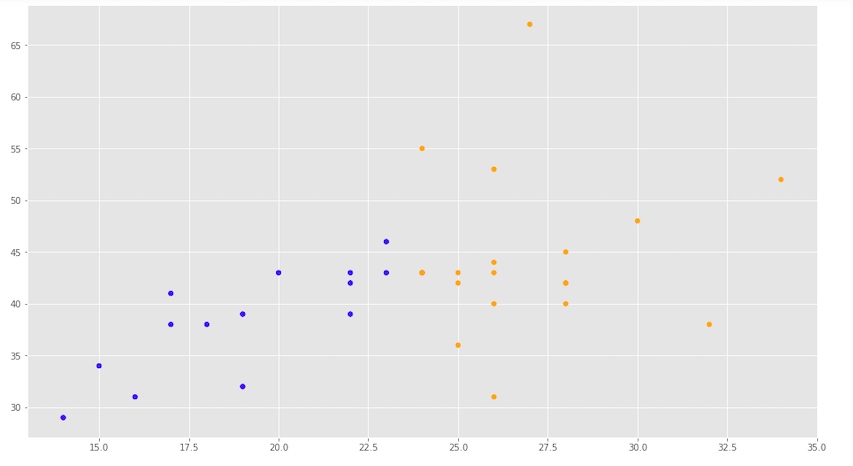
Empleando scatter mostramos los puntos coloreados, separando los colores a partir de la media de vendedores (23)

En este punto creamos nuestra recta de regresion y visualizamos los coeficientes que la componen nuestra recta.
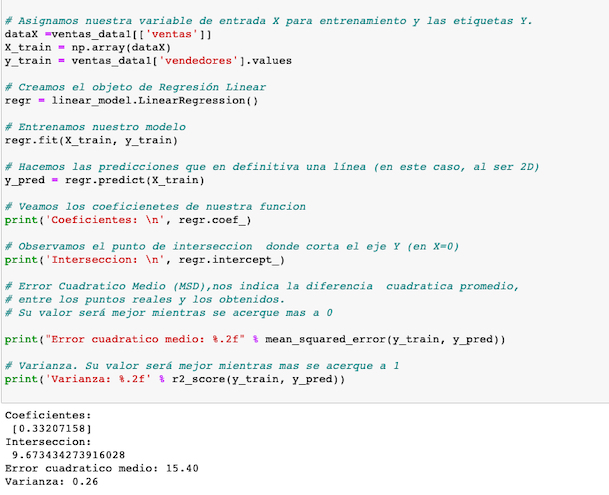
Nuestro error cuadrático no es elevado pero es alto y nuestra varianza esta más cerca de 0 que de 1, por lo que este modelo tal vez podría mejorarse.
La intersección (b), tiene un valor de 9,67…. donde se corta la recta cuando el valor en X es 0
En función de observar el comportamiento del modelo, asignamos valores diferentes para ver su comportamiento

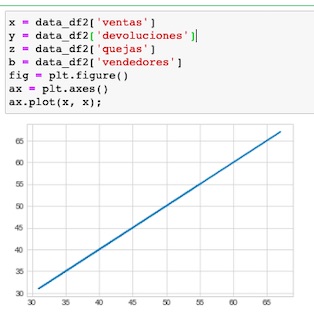
Ahora visualicemos la recta dentro de nuestro gráfico
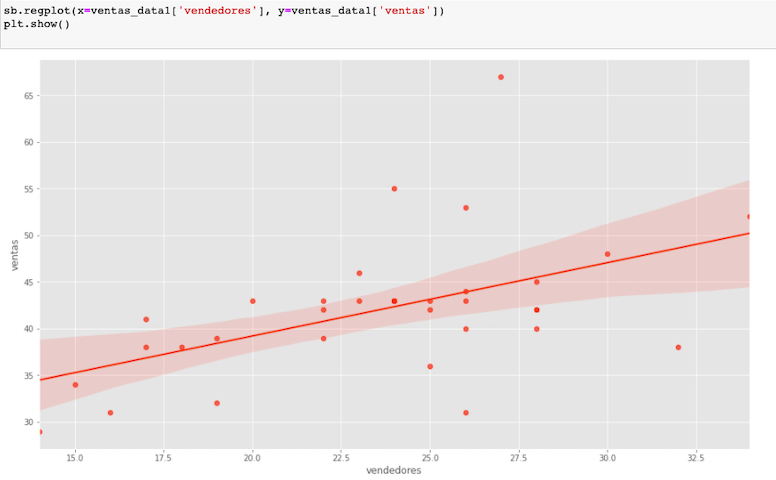
Podemos observar nuestros datos de diferentes formas, en este caso con la librería seaborn, vemos el comportamiento de los datos en los diferentes periodos y su relación.
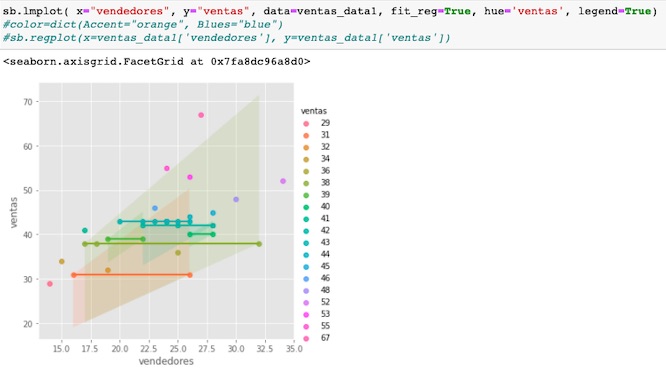
Para mejorarla tenemos varios caminos, podemos aplicar métodos como el gradiente, podemos hurgar en los datos y añadir más variables predictivas, referidas por ejemplo a la competencia, la innovación o la aceptación de los productos, pasando de una regresión simple a una regresión múltiple, podríamos también ampliar la cantidad de registros buscando mas años, desechar los valores extremos, etc.
En otros artículos iré aplicando algunos de estos métodos, haciendo referencia a estos mismos datos.
Espero modestamente que este artículo, sirva de ayuda a alguien.
Gracias
«El amor es la guerra perdida, entre el sexo y la risa»
R.Arjona